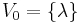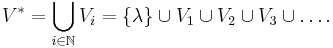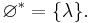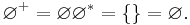Kleene star
In mathematical logic and computer science, the Kleene star (or Kleene operator or Kleene closure) is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*. It is widely used for regular expressions, which is the context in which it was introduced by Stephen Kleene to characterise certain automata, where it means "zero or more".
- If V is a set of strings then V* is defined as the smallest superset of V that contains λ (the empty string) and is closed under the string concatenation operation. This set can also be described as the set of strings that can be made by concatenating zero or more strings from V.
- If V is a set of symbols or characters then V* is the set of all strings over symbols in V, including the empty string.
That is, V* is the collection of all possible finite-length strings generated from the strings in V.
The operators are used in rewrite rules for generative grammars.
Contents |
Definition and notation
Given
define recursively the set
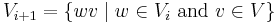 where
where 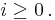
If V is a formal language, then Vi, the i-th power of the set V, is a shorthand for the concatenation of set V with itself i times. That is, Vi can be understood to be the set of all strings that can be represented as the concatenation of i strings in  .
.
The definition of Kleene star on V is
Additionally, the Kleene Star is used in Optimality Theory.
Kleene plus
In some formal language studies, (e.g. AFL Theory) a variation on the Kleene star operation called the Kleene plus is used. The Kleene plus omits the 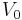 term in the above union. In other words, the Kleene plus on
term in the above union. In other words, the Kleene plus on  is
is 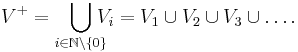
Examples
Example of Kleene star applied to set of strings:
- {"ab", "c"}* = {λ, "ab", "c", "abab", "abc", "cab", "cc", "ababab", "ababc", "abcab", "abcc", "cabab", "cabc", "ccab", "ccc", ...}.
Example of Kleene star applied to set of characters:
- {'a', 'b', 'c'}* = {λ, "a", "b", "c", "aa", "ab", "ac", "ba", "bb", "bc", "ca", "cb", "cc", ...}.
Example of Kleene star applied to the empty set:
Example of Kleene plus applied to the empty set:
Note that for every set L, 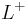 equals the concatenation of L with
equals the concatenation of L with 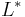 . In contrast,
. In contrast, 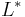 can be written as
can be written as  . The operators
. The operators 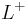 and
and 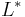 describe the same set if and only if the set L under consideration contains the empty word.
describe the same set if and only if the set L under consideration contains the empty word.
Generalization
Strings form a monoid with concatenation as the binary operation and λ the identity element. The Kleene star is defined for any monoid, not just strings. More precisely, let 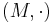 be a monoid, and
be a monoid, and 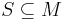 . Then
. Then 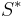 is the smallest submonoid of
is the smallest submonoid of  containing
containing  ; that is,
; that is, 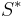 contains the neutral element of
contains the neutral element of  , the set
, the set  , and is such that if
, and is such that if 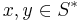 , then
, then 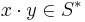 .
.
See also
- A* search algorithm
- Kleene algebra
- Extended Backus-Naur form
- Pumping lemma
- Star height
- Optimality Theory
- Formal grammar
- Finite automata
- Arden's Rule
References
The definition of Kleene star is found in virtually every textbook on automata theory. A standard reference is the following: